All exponential function graphs have the same shape, which may nevertheless be rotated, stretched or rotated to give some other exponential graph.
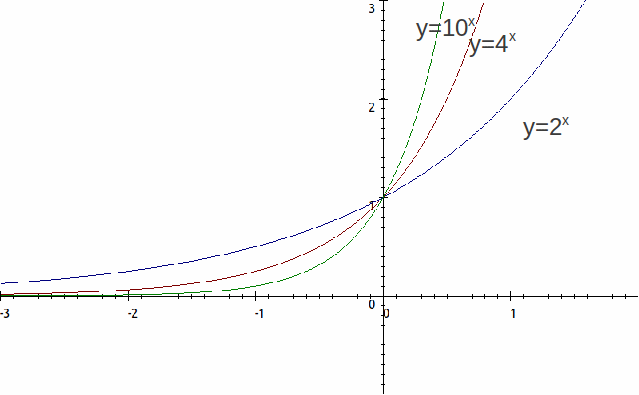
The above graphs of
and
are the graph
compressed in the
– direction. For example we can write
The graph is compressed in the- direction by the factor
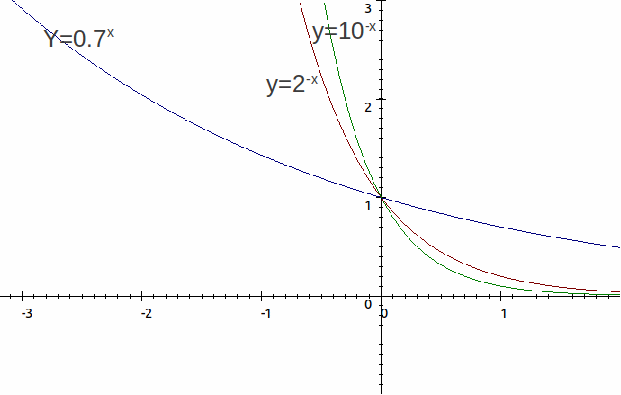
The above graphs are the reflections of the graphs graphs
andin the
- axis. The same transformation is achieved by making the swap
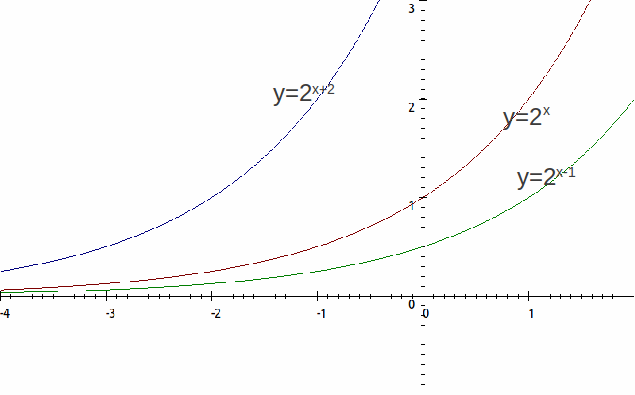
The transformation above are translations of the exponential curveby 2 to the left to give
and a translation of 1 to the right to give
Notice that a negative- transformation by two becomes a
in the equation of the graph, and a positive translation of by
becomes a
in the equation of the graph. This is because these particular transformations are– transformations, and– transformations are always counter intuitive.
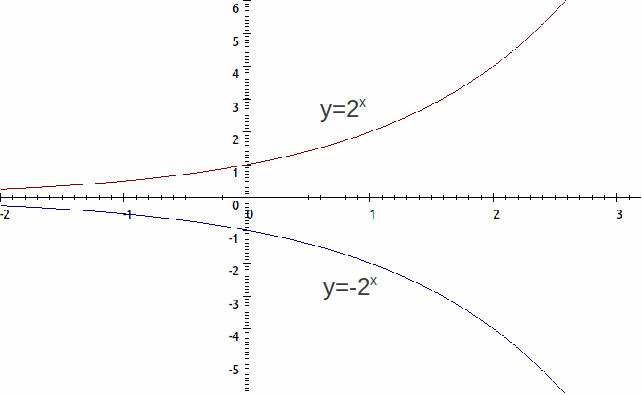
The graph of
above is the reflection of the graphin the– axis. This simple introduces a factor ofin the equation of
to give
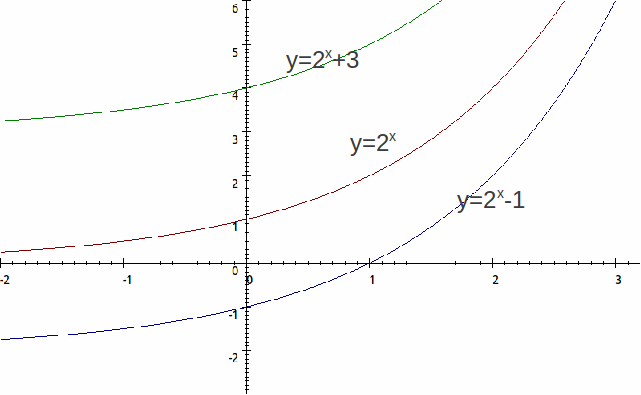
The graphis transformed above by moving up by 3 and down by 1 (– transformations) respectively. The equation becomes
and
respectively.