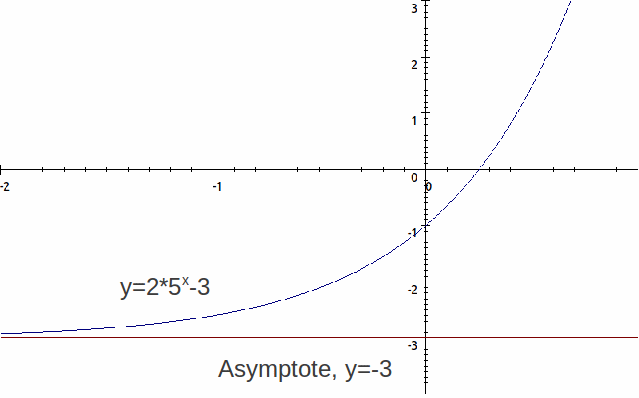
We can usually sketch exponential graphs by finding the asymptotes and the intersections of the graph with the axes. This is because all exponential graphs have the same basic shape. Any exponential curve can be obtained by reflecting, rotating and stretching.
To find the intersections with the axis, put each coordinate equal to 0.
If
we find the intersection with the
– axis by putting
We find the
– intersection by putting
This has no real solution but since
tends to 0 fortending to
we can take the– intercept to be at
To find the equation of the asymptote(s) putandsuccessively equal to
Putting
implies
and vice versa, so this gives us no asymptote. Put
to get
Putting
returns nothing forsince
has no solution for
If
we find the intersection with the– axis by putting
We find the– intersection by putting
To find the equation of the asymptote(s) putandsuccessively equal to
Puttingimpliesand vice versa, so this gives us no asymptote. Put to get
Puttingreturns nothing forsince
has no solution for
