We may be given the curve
and asked to find the set of values of
for which
We can start by sketching the curve and obtain:
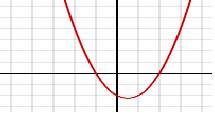
We can just read the solutions off here:
or 
We could have factorised the
expression for
to obtain
and solved
to obtain
hence the set of values of
For the quadratic above, since the coefficient of
is 1 which is positive, we know it will be a “bum” curve,so the set of solutions forwill come in two parts,or
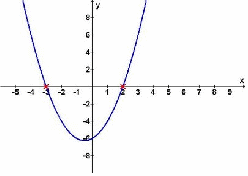
The curve shown above is
We are asked for example to find the set of values offor which
We can see from the graph that there is only one set of values:
We could have factorised the expression forto obtain
and solved
to obtain
hence we could write down the set of values of
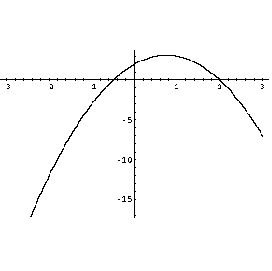
The curve shown is
We are asked
to solve
The curve is a “breast” curve and we can read off the solutionsor
We can also factorise the expression forto obtain
and solve
hence finding the set of solutions just given.