Long division of one number by another, if the divisor is not a factor, results in a decimal number, or a quotient plus a remainder. For example![]() remainder 1 or
remainder 1 or![]() 3 is the quotient and 1 the remainder. It is not just pure numbers that can undergo long division. So can polynomials. In the example below it is shown how to find the quotient and remainder of
3 is the quotient and 1 the remainder. It is not just pure numbers that can undergo long division. So can polynomials. In the example below it is shown how to find the quotient and remainder of![]() Note that we must write the numerator and denominator to include all the coefficients of
Note that we must write the numerator and denominator to include all the coefficients of![]() up to the highest power in the numerator and up to the highest power in the denominator, so that we write
up to the highest power in the numerator and up to the highest power in the denominator, so that we write![]() as
as![]()
At each stage we work to eliminate the highest power of![]() To start with the highest power of
To start with the highest power of![]() is 4: multiply the denominator
is 4: multiply the denominator![]() by
by![]() – the first term of the quotient - to get
– the first term of the quotient - to get![]() and subtract from the numerator to get
and subtract from the numerator to get![]() Now the highest power of
Now the highest power of![]() is 3. We multiply the denominator by
is 3. We multiply the denominator by![]() – the nest term of the quotient - to get
– the nest term of the quotient - to get![]() and subtract to get
and subtract to get![]() The highest power of
The highest power of![]() is 2. We multiply the denominator by 2 – the last term in the quotient - to get
is 2. We multiply the denominator by 2 – the last term in the quotient - to get![]() and subtract to get zero. Hence
and subtract to get zero. Hence![]() There is no remainder.
There is no remainder.
If instead we are finding the quotient and remainder of![]() we follow the same process, but now, as shown below, the remainder is 9 hence the division is now
we follow the same process, but now, as shown below, the remainder is 9 hence the division is now
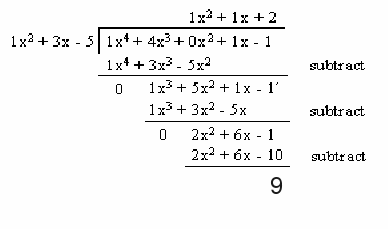
hence![]()
