The ballot problem poses the question: If, of two candidates running for office, one wins, what is the probability that the other has led at any stage during the counting process?
More precisely, suppose there are n votes cast in total and the votes are counted one by one. When all the votes are counted, candidate A has won by![]() votes. Candidate A wo
votes. Candidate A wo![]() votes and candidate B won
votes and candidate B won![]() votes (
votes (![]() ).
).
We assume each vote is cast for candidate A with probability![]() (and for candidate B with probability
(and for candidate B with probability![]() ) and the order of counting is independent of the candidate for which the votes are cast. For k ≤ n, let
) and the order of counting is independent of the candidate for which the votes are cast. For k ≤ n, let![]() be the number of votes received by candidate A minus the
be the number of votes received by candidate A minus the
number of votes received by candidate B in the first![]() ballots. When the
ballots. When the![]() vote is counted,
vote is counted,![]() increases by 1 if the vote was for candidate A, or decreases by 1 if the vote was cast for candidate B. The votes are independent of each other and
increases by 1 if the vote was for candidate A, or decreases by 1 if the vote was cast for candidate B. The votes are independent of each other and![]() so
so![]()
![]() is (the beginning of) a simple random walk. The probability of increasing by 1 is
is (the beginning of) a simple random walk. The probability of increasing by 1 is![]() which is not symmetric if
which is not symmetric if![]()
The ballot problem can now be restated as follows:
Find the probability that![]() for all
for all![]() given
given![]() ?
?
We must find![]() where F denotes the set of trajectories that stay non-negative and G the set of those that reach m at time n. Each trajectory in G has (n + m) over 2 moves right and (n − m) over 2 moves left, so its probability weight is always equal to
where F denotes the set of trajectories that stay non-negative and G the set of those that reach m at time n. Each trajectory in G has (n + m) over 2 moves right and (n − m) over 2 moves left, so its probability weight is always equal to![]() Therefore,
Therefore,
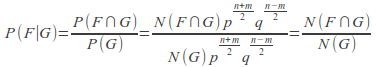
The number of paths in![]()
![]() is equal to
is equal to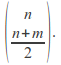 We count the number of paths in
We count the number of paths in![]() The paths in
The paths in![]() form a portion of all the paths in
form a portion of all the paths in![]() which don’t reach −1, so
which don’t reach −1, so
that![]() where
where![]() is the set of all paths which finish at
is the set of all paths which finish at![]() but cross or touch the level −1 in the process. We can use the reflection principle to find
but cross or touch the level −1 in the process. We can use the reflection principle to find![]() The reflection of any path in H in −1 after its first hitting time of that level produces a path that starts at 0 and ends at
The reflection of any path in H in −1 after its first hitting time of that level produces a path that starts at 0 and ends at![]() Conversely, the same procedure applied to such a path yields a path in
Conversely, the same procedure applied to such a path yields a path in![]() The number of paths from 0 to
The number of paths from 0 to![]() is equal to
is equal to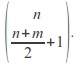 Putting everything together, we get
Putting everything together, we get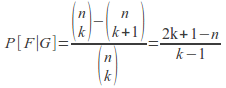 where
where![]()
