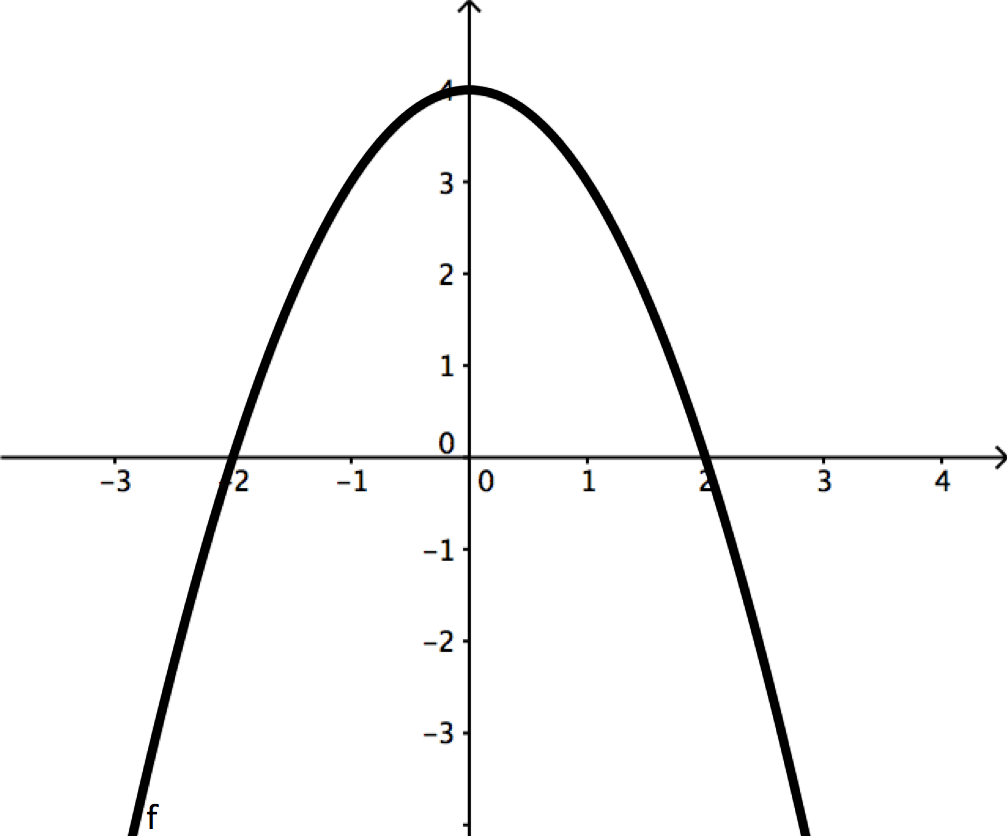
\[y=4-x^2\]
.The curve intersects the x - axis at
\[x=-2\]
and \[x=2\]
.The area between the curve and the x -axis between the x values -2 and 2 is
\[\int^2_{-2} x^2 dx = [\frac{x^3}{3}]^2_{-2} = \frac{2^3}{3}- \frac{(-2)^3}{3}=\frac{8}{3}- (- \frac{8}{3})=\frac{16}{3} \]
