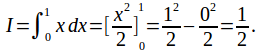Some integrals cannot be calculated exactly. A good example is![]() The integral exists and is equal to the area A below.
The integral exists and is equal to the area A below.
In examples like this it is useful to be able to calculate lower and uppoer bounds for the value of an integral. We can find a lower bound by dividing the interval of integration on the![]() axis into sunbintervals
axis into sunbintervals![]() and finding the minimum value of the function,
and finding the minimum value of the function,![]() on this interval. Form rectangles with base of length
on this interval. Form rectangles with base of length![]() and height
and height![]() and area
and area![]() and add these to get a lower bound for the value of the integral,
and add these to get a lower bound for the value of the integral,![]()
To find an upper bound find the maximum value of the function, F-i on each subinterval![]() Form rectangles of base
Form rectangles of base![]() and height F-i and area
and height F-i and area![]() and add these to get a upper bound for the value of the integral,
and add these to get a upper bound for the value of the integral,![]()
To illstrate, find upper and lower bounds for![]() on
on![]() by dividing the interval
by dividing the interval![]() into 5 subintervals
into 5 subintervals![]()
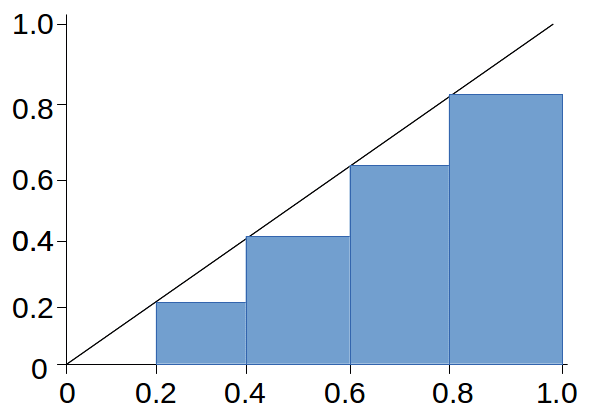
A lower bound is found from the diagram below:
![]()
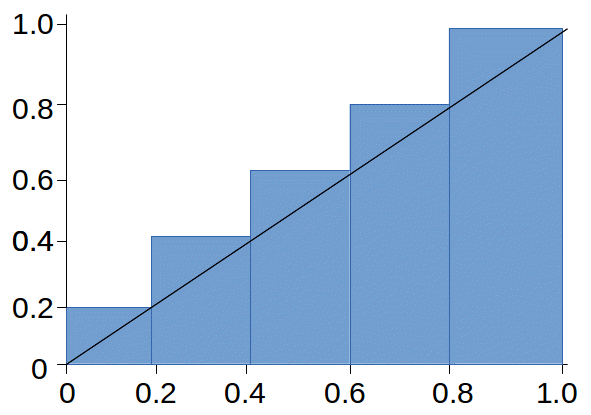
An upper bound for the integral is found from the diagram below.
![]()
Compare these bound with the actual value