Consistent, Inconsistent and Degenerate Systems of Linear Equations
It is conveninet to give some definitions:
A system of equations is degenerate if more than one set of solutions equations and non degenerate if only one set of solutions exists.
A system of equations is inconsistent if no solutions exists.
A system of equations is consistent if solutions exist – either a unique set of solutions or more than one.
The definitions can be illustrated with matrices.
We can represent the simultaneous equations
in matrix form as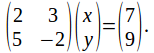
This system of equations is consistent and non – degenerate. It is consistent and non – degenerate because the coefficient matrix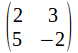
is invertible, so a solution exists. We can write the solution as
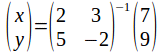- this is unique so the system is non degenerate.
The system of equations
is inconsistent.
It is inconsisten because if we double the first equation, we obtain
4x+6y=14
but from the second equation,
For a system of equations to be inconsistent it must be the case that the coefficient matrix has zero determinant, and no inverse. The coefficient matrix for these simultaneous equations is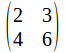
with determinant 2*6-3*4=0.
It is possible however for the coefficient matrix to have determinant zero, but for the system to have solutions – many solutions in fact. The system of equations
has many solutions:
and
and
In fact any number
will return a value
such that
is a solution of the equations.
We can generalise to higher orders. A system of linear equations has:
A unique solution if the determinant of the coefficient matrix is not equal to zero.
No solutions if the determinant of the coefficient matrix is zero but no equation can be expressed in terms of the others. For the last example above the second equation can be expressed in terms of the first by doubling it, and the first equation can be expressed in terms of the second by halving it.
Many solutions if the determinant of the coefficient matrix is zero and one equation can be expressed in terms of the others.
