A region in the complex plane is a non - empty, open, connected set. The following are all regions.
Any open disc
Any open half plane
The complement![]() of any closed disc
of any closed disc![]()
Any open annulus
The set![]() itself
itself
Any open rectangle, triangle, pentagon or similar shape
Any open, connected set with a finite number of points excluded
Proving the last of these is a set is quite easy.
Theorem
If![]() is a region and
is a region and![]() then
then![]() is also a region.
is also a region.
Proof
Since R is a region it contains an open disc centred on![]() so
so![]() is non – empty. Also
is non – empty. Also![]()
![]() is closed in
is closed in![]() so
so![]() is open and
is open and![]() is open as the intersection of two open sets.
is open as the intersection of two open sets.
Suppose that![]() Since
Since![]() and
and![]() is a region, we can join
is a region, we can join![]() and
and![]() by a path
by a path![]() in
in![]() and the path also lies in
and the path also lies in![]() if
if![]()
If however![]() lies on
lies on![]() then choose an open disc
then choose an open disc![]() (possible since R is a region) and modify
(possible since R is a region) and modify![]() inside this disc to avoid
inside this disc to avoid![]()
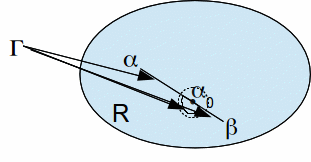
The resulting path joins![]() and
and![]() in
in![]() so
so![]() is connected and
is connected and![]() is a region.
is a region.
We can apply this region recursively to exclude any finite number of points![]()
