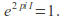Given two groups
and
a group homomorphism from
to
is a function
such that for all
where the group operation on the left hand side of the equation is that of
and on the right hand side that of
maps the identity element
of G to the identity element
of
and it also maps inverses to inverses:
We define the kernel of h to be the set of elements in G which are mapped to the identity in H
and the image of h to be
The kernel is a normal subgroup ofsince
and the image is a subgroup of H. The homomorphism h is injective if and only if
Examples
-
The cyclic group
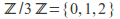and the group of integers
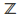under addition. The map
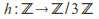with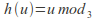
is a group homomorphism. It is surjective and the kernel consists of all multiples of 3.
-
The exponential map yields a group homomorphism from the group of real numbers
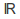under addition to the group of non-zero real numbers
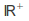- the image - under multiplication. The kernel is
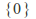and the image consists of the positive real numbers.
-
The exponential map also yields a group homomorphism from the group of complex numbers
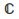with addition to the group of non-zero complex numbers
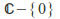with multiplication. This map is surjective and has the kernel
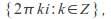sine