A morphism![]() is a mapping between sets. The different types of morphism are
is a mapping between sets. The different types of morphism are
-
Homomorphism: preserves the structure (e.g.
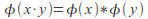 ) where
) where and
and are the operations on the domain and codomain respectively. For example exp is a morphism from
are the operations on the domain and codomain respectively. For example exp is a morphism from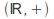 to
to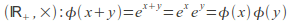 where
where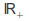 is the set of positive real numbers.
is the set of positive real numbers. -
Epimorphism: a homomorphism that is surjective or onto.
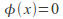 is a homomorphism from
is a homomorphism from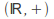 onto the set consisting of the single element 0. (with the operation of either ordinary addition or ordinary multiplication.)
onto the set consisting of the single element 0. (with the operation of either ordinary addition or ordinary multiplication.) -
Monomorphism: a homomorphism that is injective or one to one. The homomorphism
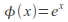 illustrated above is a monomorphism.
illustrated above is a monomorphism. -
Isomorphism: a homomorphism that is bijective (one to one and onto); isomorphic objects are equivalent.
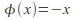 is an isomorphism from
is an isomorphism from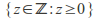 to the set
to the set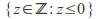 with the operation of addition on both domain and codomain.
with the operation of addition on both domain and codomain. -
Endomorphism: a homomorphism from a set to a subset of itself. Eg
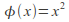 is an endomorphism from
is an endomorphism from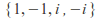 to
to 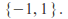
-
Automorphism: a bijective endomorphism (an isomorphism from an set onto itself, essentially just a re - labeling of elements):
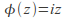 where z is a complex number of magnitude 1 is an isomorphism. The effect of
where z is a complex number of magnitude 1 is an isomorphism. The effect of is to rotate
is to rotate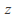 by
by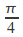 anticlockwise about the origin.
anticlockwise about the origin.
Every morphism send the identity in the domain to the identity in the codomain. This is easy to prove:
If![]() is the identity element in the domain with operation
is the identity element in the domain with operation![]() then
then
![]() so
so![]() is the identity element in the codomain.
is the identity element in the codomain.
The relationship between the different types of morphism may be written
automorphisms![]() isomorphisms
isomorphisms![]() monomorphisms
monomorphisms![]() homomorphisms.
homomorphisms.
Endomorphisms do not fit easiliy into this relationship since they are not isomorphisms and must be from a set into the same set.
