A permutation group is a group
of order
whose elements are permutations of the integers
The set of all permutations is labelled
and called the symmetric group. A permutation group labelled
is usually a subgroup of the symmetric group.
As a subgroup of a symmetric group, all that is necessary for a permutation group to satisfy the group axioms is that it contain the identity, (1)(2)...(n-1), the inverse permutation of each permutation it contains, and be closed under composition of its permutations.
Consider the following set
of permutations of the set {1,2,3,4}:
-
The identity,
-
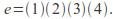
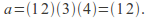The labels 1 and 2 are interchanged, 3 and 4 are fixed. -
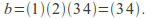The labels 1 and 2 are fixed, 1 and 2 are interchanged. -
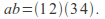This permutation interchanges 1 with 2, and 3 with 4.
forms a permutation group with each element self inverse. It is isomorphic to the Klein group.
More generally, every groupis isomorphic to a permutation group by virtue of its regular action onas a set; this is the content of Cayley's theorem.
Ifand
are two permutation groups, then we say thatandare isomorphic as permutation groups if there exists a bijective map
betweenandsuch that
with
This is equivalent toandbeing conjugate subgroups of
A 2-cycle is known as a transposition. A simple transposition inis a 2-cycle of the form
Every permutation p can be written as a product of simple transpositions; furthermore, the number of simple transpositions one can write a permutation as is the number of swaps needed to bring the n-1 numbers in the set
back to the natural orderand if the number of transpositions in p is odd or even corresponding to the oddness of p the number of swaps is also odd or even. Composing permutations has the following intuitive rules:
The set of even transposition informs a subgroup offor each