To find the equation of the image![]() of a path
of a path![]() under the reciprocal function
under the reciprocal function![]()
-
Write down an equation relating the
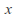 and
and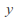 components of all points
components of all points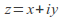 on
on 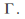
-
Replace
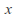 by
by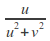 and
and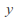 by
by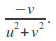 (Note that
(Note that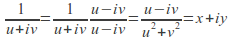 )
) -
Simplify the resulting equation to obtain an equation relating the
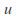 and
and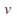 components of all points
components of all points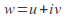 on the image
on the image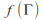
Example: Find the equation of the image of the circle![]() under the reciprocal function.
under the reciprocal function.
The centre of the circle is at![]() and the radius of the circle is 3. The cartesian equation of the circle is
and the radius of the circle is 3. The cartesian equation of the circle is![]()
Making the substitution in 2 gives
![]()
Expanding gives![]()
Collecting the first and fourth terms gives![]()
Cancelling and clearing fractions gives
![]()
Hence![]()
Completing the square gives![]()
This is the equation of a circle centre![]() with radius
with radius![]()
In general the reciprocal function sends:
a line through the origin to a line through the origin
a line not through the origin to a circle through the origin
a circle through the origin to a line not through the origin
a circle not through the origin to a circle not through the origin.
