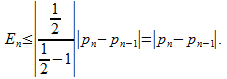An Upper Bound on the Error at Each Iteration When Finding a Root or Fixed Point

Generally, the exact value of the rootof a function(or the exact value of a fixed point) is unknown, so it is impossible to evaluate the error of iterative methods,but

we can find an upper bound on the error using the difference between two iterates.

Definition: A sequenceis called contractive if there exists a positive constantsuch that

Theorem

Ifis contractive with constantthen,

i. is convergent with limit

ii.is bounded above and

Hence, forgiven,provides an upper bound onthe error at

iteration

Example:The first fiveare given below.

K can be hard to find. It can be shown that we can takefrom the above table so