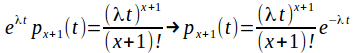Derivation of the Poisson Distribution

A probability distribution may be modelled by a Poisson distribution if events occur randomly at a constant average rate,and each occurrence of each event is independent of every other occurrence. On top of this, events may never occur in pairs, so that two events occur at the same time.

If a type of event occurs at the ratethen in a small interval of lengthwe haveso that

Suppose events occur and obey a probability distributionas described above, thenis a Poisson distribution with parameter

Letdenote no events in the time intervalthen

Therefore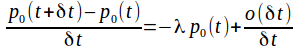

Letto give

Integration gives

so that

In general

So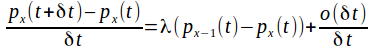

Aswe obtain

Now prove by induction.

Assume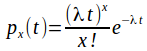and use from above

as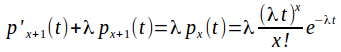

Now multiply by the integrating factorto give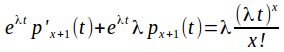

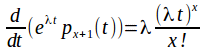
Integration now gives