Queue Waiting Time

If there is anyone in a queue at all, people will be waiting to be served. The waiting time is the the time taken for the person waiting at the back of the queue to be served. If queue is of lengthit will be the time for all these people to leave the queue and be served. If the service timesare exponential, they have the lack of memory property so at each instant the expected remaining time to serve the first person is still

The queuing time is then the sum ofindependent exponentially distributed random variables (the x people in the queue plus the one being served) and so is a Gamma distribution

For the queue in a state of equilibrium letbe the density of the queueing time and let be the density for a queue size of length

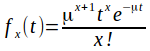for

and

so

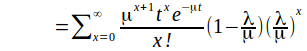
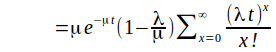
The queueing time for an individual customer is exponential with parameter