Features Of the Derivative Graph

Any function can be graph. When a function is differentiated, aderivative function is the result. This derivative function can begraphed, and features of the derivative graph may tell us somethingabout the original graph. In particular, we can identify stationarypoints and determine their nature.

Suppose a functionhasderivativethegraph of which is sketched below.

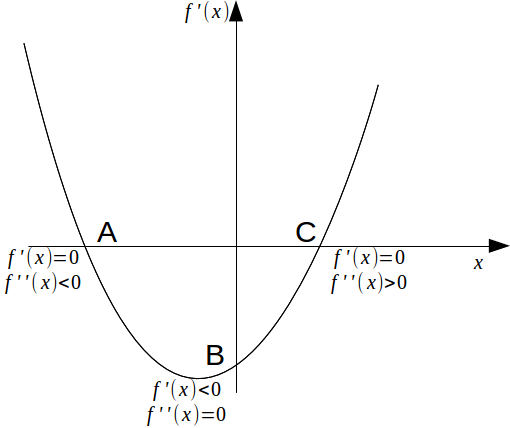
At the point A,sothe point A is a stationary point forSincethepoint A is a maximum.

At the point B,sothe point B is a point of inflection forSincethe point B is a non stationary point of inflection.

At the point C,sothe point C is a stationary point forSincethe point C is a minimum.

The graph below has three points of inflexion.

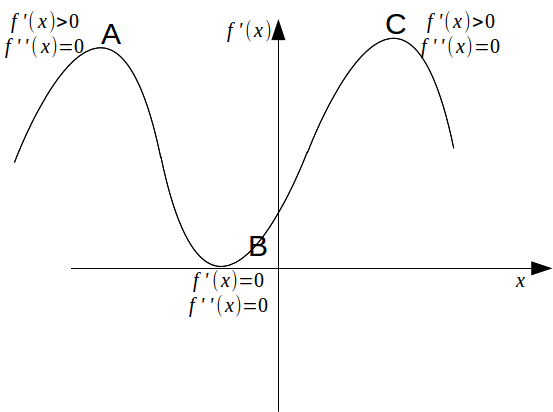
At the point A,so the point A is a point of inflexion forSincethepoint A is a non stationary point of inflexion.

At the point B,sothe point B is a point of inflection forSincethe point B is a stationary point of inflection.

At the point C,sothe point C is a point of inflexion forSincethepoint A is a non stationary point of inflexion.