To compose two functions![]() and
and![]() is to use the result of one function in the other. If
is to use the result of one function in the other. If![]() and
and![]() then to find to compose
then to find to compose![]() and
and![]() with
with![]() with
with![]() being performed first, find
being performed first, find![]() then find
then find![]()
We can write this as![]() or
or![]() In general, the composition of
In general, the composition of![]() with
with![]() with
with![]() being performed first is written
being performed first is written![]() or
or![]() or simply
or simply![]() (this is distinct from the product of
(this is distinct from the product of![]() and
and![]() written
written![]() or
or![]() ).
).
You may think of![]() being used as the argument of
being used as the argument of![]() so that if
so that if![]() then
then![]() then if
then if![]()
![]()
The composition of functions has some important properties.
-
If a function
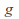 is the inverse of a function
is the inverse of a function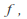 so that
so that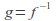 then
then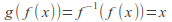 and
and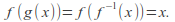
-
Composition of functions is associative so that
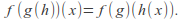 If
If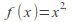
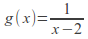 and
and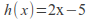 then
then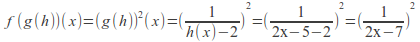 and
and 
We can compose functions graphically.![]() and
and![]() as shown below,
as shown below,
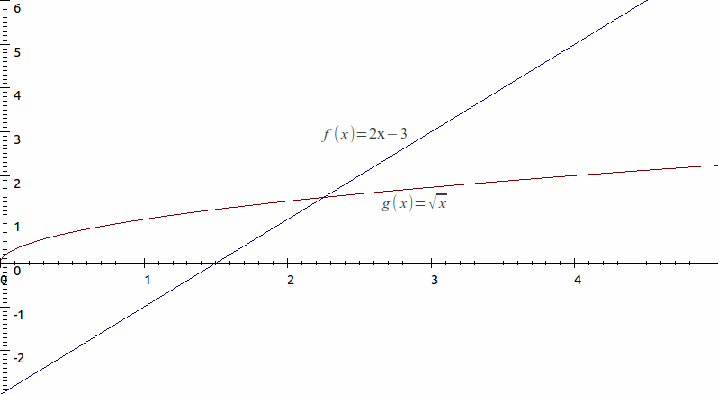
Then![]()
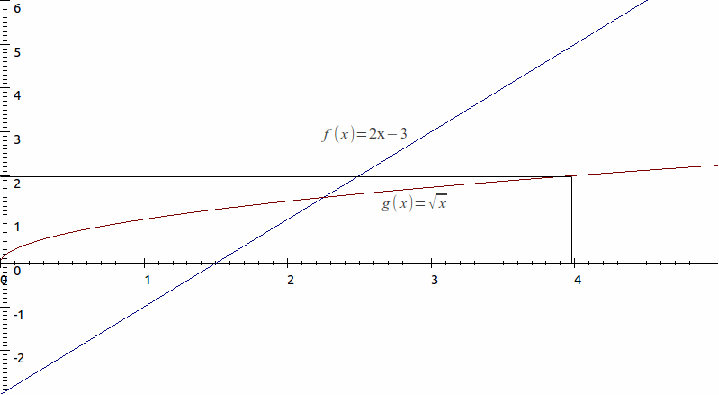
and![]()
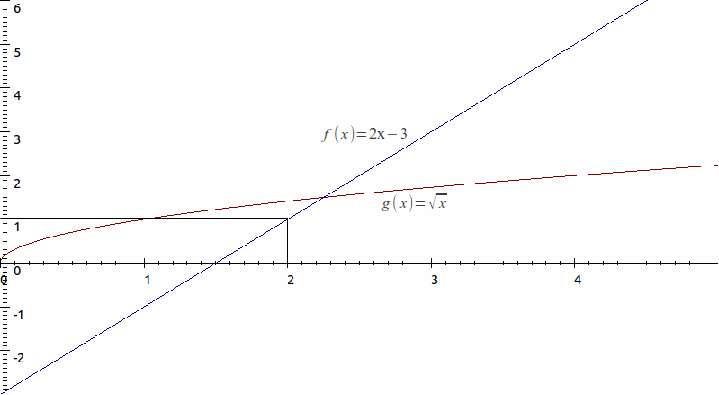
So that![]()
