Sketching Quadratic Graphs
It is often not necessary to plot quadratics by drawing up a table of x values and corresponding y values. Often a few points will suffice to obtain the main features of the graph and sketch it. The main features of a quadratic graph are:
The vertex. This is the maximum or minimum of the graph. A quadratic has eithe a maximum or a minimum, and there is only one of them. If the equation of the graph is
and 
then the vertex is a maximum and the coordinates of the vertex are
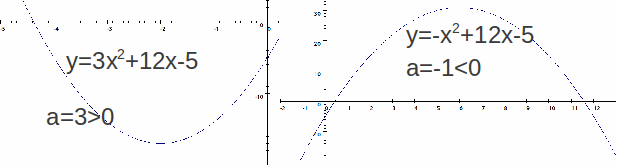
The graph above left has a vertex at
This is a maximum because
The graph above right has a vertex at
The equation of the line of symmetry. For a quadratic graph
the equation of the line of symmetry is
For
(above left), this gives
The
– intercept. This is easily found by substituting
in the equation of the graph
Forwe obtain
The
- intercept(s), if they exist. Not every quadratic has- intercepts. Forintercepts to exist, the equation
must have real solutions. Since the solutions are given by
we must have that:
for a unique solution. The graph touches the– axis but does not cross it.
for two distinct solutions. In this case the two solutions are given by
and
The- intercepts for the graphare
and 
If the quadratic factorises then we may find the intercepts by setting each factor equal to 0. For example
factorises as
and
