Some functions have symmetry about the origin.
If the function is such that![]() then the graph of the function ihas reflectional symmetry in the y – axis and the function is said to be even.
then the graph of the function ihas reflectional symmetry in the y – axis and the function is said to be even.
If the function is such that![]() then the graph of the function ihas rotational symmetry of order two about the origin and the function is said to be odd.
then the graph of the function ihas rotational symmetry of order two about the origin and the function is said to be odd.
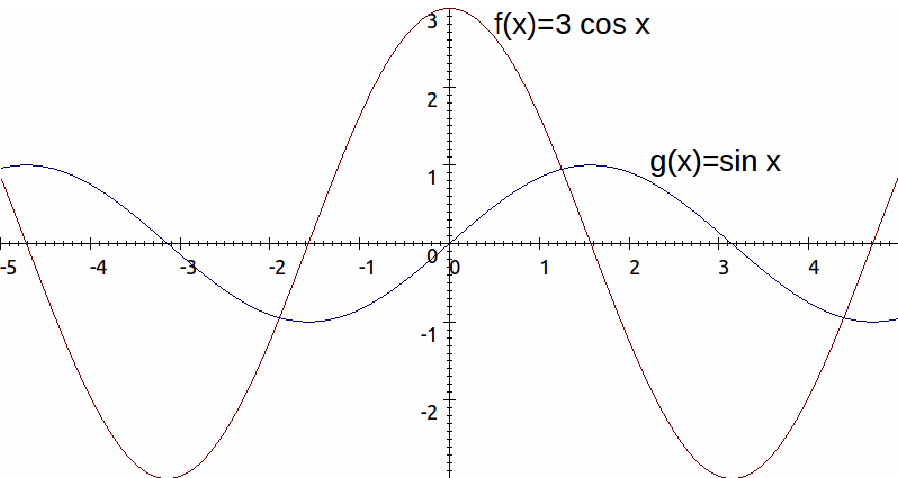
In the diagram below![]() is even and
is even and![]() is odd.
is odd.
It is not necessary for a function to be either even or odd.![]() is neiher even or odd, but every function can be written as an even component plus and odd component.
is neiher even or odd, but every function can be written as an even component plus and odd component.
If![]() and
and![]() then
then![]() is even and
is even and![]() is odd, and
is odd, and![]()
It is often quite easy to test a function for oddness or evenness.
![]() so
so![]() so
so![]() is odd.
is odd.
![]() so
so![]() so
so![]() and
and![]() is even.
is even.
![]() so
so![]() or
or![]() so
so![]() is neither odd nor even.
is neither odd nor even.
